NumPy基礎プログラミング

2020/05/21

「AI CORE XスターターキットとOpenVINO™ですぐに始めるディープラーニング推論」シリーズの５回目記事です。

このシリーズは、「ディープラーニングとは何か」から始まり、「各種ツールの使い方」「プログラミング基礎」「プログラミング応用・実践」までをステップバイステップでじっくり学び、自分で理解してオリジナルのAIアプリケーションが作れるようになることを目指しています。

第５回目はディープラーニングでプログラミングの肝となるNumPyを学びます！前半は配列としての基礎、後半は画像データとの関連について学びます。

【 目次 】

NumPyとは

NumPyとは数値計算を効率的に行うための拡張モジュールです。言い換えると、ベクトルや行列などの多次元配列を高速に計算するためのライブラリです。また画像データとも密接な関係があります。
OpenCVと同様に、NumPyを使用するためにはnumpyモジュールをimportする必要があります。

import numpy

上記のimportでも全く問題ないのですが、慣例的に np という別名を付けることが一般的ですので、本サイトでもこちらのインポート形式を使います。

import numpy as np

ndarray

NumPyで扱う多次元配列は ndarray という名称です。（N-dimensional array の略）
ndarrayはPython基礎で習ったリストと関連性があります。リストと表記が似ていて混同しやすいので注意しましょう。
ちなみに、プログラムのソースコードには ndarray という関数は出てきません。

import numpy as np
 
a = [10, 20, 30]
b = np.array(a)
print(b)
 
# 実行結果 
# [10 20 30] 

上記のソースコードの解説です。
変数 a はPythonプログラミング基礎で学んだ「リスト」です。
変数 b がndarrayです。 np.arrayという関数を使ってリストをndarrayに変換しています。
最後にprintで表示しています。実行結果を見ると、ndarrayはリストと異なり、カンマが無いのが特徴です。

初期化

ndarrayの初期化方法です。既に先ほどのコードで出ていますが、np.arrayを使って行います。
ここでは、具体的にリストとndarrayの違いを比較しながら確認してゆきましょう。
実行結果を見ると分かりますが、リストにはカンマがついていますが、ndarrayにはカンマが無いことが確認できます。

import numpy as np
 
#リスト 
a = [10, 20, 30]
print(a)
 
#ndarray 
b = np.array([10, 20, 30])
print(b)
 
# 実行結果 
# [10, 20, 30] 
# [10 20 30] 

次に、２次元の場合との比較です
ndarrayの結果は途中で改行が入っています。

import numpy as np
 
#リスト 
a = [[10, 20, 30], [40, 50, 60]]
print(a)
 
#ndarray 
b = np.array([[10, 20, 30], [40, 50, 60]])
print(b)
 
# 実行結果 
# [[10, 20, 30], [40, 50, 60]] 
# [[10 20 30] 
# [40 50 60]] 

ndarrayの初期化は、これまでのコードで書いてきたように np.array(list)で行いますが、要素に規則性がある場合は、別の方法で初期化も可能ですので、１つご紹介します

全てゼロで初期化

np.zerosを使うと指定した形状で要素が全て0であるndarrayを生成できます。形状はタプルで指定します。「形状」とは、どのような配列の構成にするかということです。また後ほど説明します。実際に例を見た方が分かりやすいです。以下は 形状(2, 3) のndarrayを np.zerosを使って生成する例です

import numpy as np
 
a = np.zeros((2, 3))
print(a)
 
# 表示結果 
# [[0. 0. 0.] 
#  [0. 0. 0.]] 

ndarrayの各値のデータ型が小数の場合、小数点以下の数値がなくても、ドット.が付くのが特徴的です。

要素参照

要素参照についても、具体的にリストとndarrayの違いを比較しながら確認してゆきましょう。
１次元の場合の要素参照はリストもndarrayも同じです。

import numpy as np
 
#リスト 
a = [10, 20, 30]
print(a[1])
 
#ndarray 
b = np.array([10, 20, 30])
print(b[1])
 
# 表示結果 
# 20 
# 20 

２次元の場合、表示結果は同じですが、参照方法が異なることに注目してください。
実はndarrayも b[1][2] という書き方でもOKなのですが、ndarrayの場合は慣例的に b[1, 2] という書き方をします。

import numpy as np
 
#リスト 
a = [[10, 20, 30], [40, 50, 60]]
print(a[1][2])
 
#ndarray 
b = np.array([[10, 20, 30], [40, 50, 60]])
print(b[1, 2])
 
# 表示結果 
# 60 
# 60 

最大値のインデックス

np.argmax は 配列（リストやndarray）の中で最大値の要素のインデックスを値で返します。

import numpy as np
 
a = np.array([10, 50, 40, 30, 20])
b = np.argmax(a)
print(b)
 
# 表示結果 
# 1 

配列の中の最大値は 50 ですが、そのインデックスが 1 であるため、このような実行結果になります。最大値そのものではなく、最大値の位置にあるインデックスを返すというのがポイントです。

ソートのインデックス

np.argsortを使うと、配列（リストやndarray）を昇順に並べたときのインデックスをndarrayで返します。
この説明だけだと分からないと思いますので、具体的にサンプルソースで確かめてみましょう

import numpy as np
 
a = np.array([10, 50, 40, 30, 20])
b = np.argsort(a)
print(b)
 
# 表示結果 
# [0 4 3 2 1] 

np.argsortはちょっと分かりにくいですが、落ち着いて見れば理解できます。
[10, 50, 40, 30, 20] を昇順に（つまり小さい方から大きい方へと）並べると[10, 20, 30, 40, 50] になるのは分かると思います。このとき元々のリストに [0, 1, 2, 3, 4] というインデックスのラベルが付いていて、昇順に並べた後の結果のラベルを見てみると [0, 4, 3, 2, 1]になるという流れです。

形状

ndarrayには「次元」以外の要素として「形状」があります。形状は各次元における要素の数のことです。shapeを使うと、形状を表示させることができます。

まずは１次元の例です。
実行してみると、中途半端なカンマで終わっていますが、要素数が 4 ということで合っていると思います。１次元の場合はこのような (x,) という中途半端なカンマで表示されます。

import numpy as np
 
a = np.array([1, 2, 3, 4])
print(a.shape)
 
# 表示結果 
# (4,) 

今度は２次元の例です。実行してみると(3, 4) ということで一致しています。

import numpy as np
 
a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
print(a.shape)
 
# 表示結果 
# (3, 4) 

次に３次元の例。長いので途中で改行しました。結果は (2, 3, 4 ) で一致しています。

import numpy as np
 
a = np.array([[[ 1,  2,  3,  4], [ 5,  6,  7,  8], [ 9, 10, 11, 12]], 
              [[13, 14, 15, 16], [17, 18, 19, 20], [21, 22, 23, 24]]])
print(a.shape)
 
# 表示結果 
# (2, 3, 4) 

ndarrayと画像データ

冒頭で述べたようにndarrayと画像データは密接な関係があります。これまで使ってきた変数と画像の型を比較したいと思います。
type関数を使うと、変数の型を見ることができます。

import numpy as np
 
a = 100
b = 3.14159
c = 'deep learning'
d = [10, 20, 30]
e = np.array([10, 20, 30])
 
print(type(a))
print(type(b))
print(type(c))
print(type(d))
print(type(e))
 
# 表示結果 
# <class 'int'> 
# <class 'float'> 
# <class 'str'> 
# <class 'list'> 
# <class 'numpy.ndarray'> 

整数(int)、小数(float)、文字列(str)、リスト(list)、ndarray(numpy.ndarray)と表示されています。
次にOpenCVプログラミング基礎で使った cat.jpg を cv2.imread して型と形状を見てみましょう

import cv2
 
image_file = 'cat.jpg'
img = cv2.imread(image_file)
 
print(type(img))
print(img.shape)
 
# 表示結果 
# <class 'numpy.ndarray'> 
# (533, 800, 3) 

実は cv.imread で読み込まれた画像はndarrayに変換されていました。
そして形状をみると (533, 800, 3) であり、(高さ, 幅, カラーチャンネル)を示しています。カラーチャンネルは 青と緑と赤の三色の3です。

これを利用して、個別に画像の幅を取得したい場合は形状の0番目の要素、高さを取得したい場合は形状の1番目の要素を指定すれば得られます。

import cv2
 
image_file = 'cat.jpg'
img = cv2.imread(image_file)
 
print(img.shape[0])
print(img.shape[1])
 
# 表示結果 
# 533 
# 800 

このように、画像はそのままndarrayとして取り扱えるということが理解できたかと思います。

スライス

一般的な用語としてスライスとは薄く切り出すことですが、Pythonにおいては厚い薄いに関係なく「切り出す」という意味になります。具体的には配列から複数の要素を一気に切り出します。

リストのスライス

リスト名[n:m]を使うとリストから条件にあった要素全てを取り出すことができます。
取り出される要素は n ～ m-1 番目です。 m-1 というのがちょっとややこしいですね。
では、実際のプログラムで確かめてみましょう。

a = [10, 20, 30, 40, 50, 60, 70, 80, 90, 100]
b = a[2:5]
print(b)
 
# 実行結果 
# [30, 40, 50] 

どうでしょう、実行してみると理解しやすいと思います。
実は n もしくは m を省略することもできます。
n を省略した場合は 最初 ～ m-1 まで、 m を省略した場合は n ～ 最後までを取り出します。

a = [10, 20, 30, 40, 50, 60, 70, 80, 90, 100]
 
b = a[:5]
print(b)
 
c = a[2:]
print(c)
 
# 実行結果 
# [10, 20, 30, 40, 50] 
# [30, 40, 50, 60, 70, 80, 90, 100] 

反転リスト [::-1]

リスト名 [::-1] という書き方で、反転したリストを得ることができます。
スライスは [n : m : s] という書き方や、負の数を指定したりできます。詳細説明は割愛しますが、この複合技が [::-1] という訳です

a = [10, 20, 30, 40, 50, 60, 70, 80, 90, 100]
b = a[::-1]
print(b)
 
# 実行結果 
# [100, 90, 80, 70, 60, 50, 40, 30, 20, 10] 

記号はややこしいですが、やっていることは分かりやすいかと思います。
[::-1] という記号が出てきたときに「反転リスト」だと思い出せればOKです。

画像への応用

スライスはリストだけでなく、ndarrayにも適用可能です。
先程と同様で、ndarrayにて [n:m]を使うと n ～ m-1 番目の要素が取り出されます。
実際のプログラムで確かめてみましょう。

import numpy as np
 
a = np.array([0, 10, 20, 30, 40, 50, 60, 70, 80, 90])
print(a[3:8])
 
# 表示結果 
# [30 40 50 60 70] 

これまでのコードは１次元のスライスでしたが、２次元や３次元でも同様に使うことができます。
スライスを画像データに適応すると、画像の１部分だけの取得が可能になります。

import cv2
 
image_file = 'cat.jpg'
img = cv2.imread(image_file)
 
cv2.imshow('image', img[200:350, 100:300])
 
cv2.waitKey(0)
cv2.destroyAllWindows()

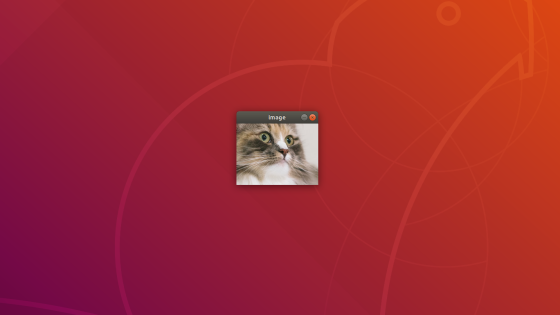
猫の顔の部分だけが表示されたと思います。
このようにスライスを画像に適用すると、非常に簡単に画像の１部分のみを切り出すことが出来ます。

ndarrayの順番は [高さ方向, 幅方向] であることに注意してください。

次元

これまでも、1次元、2次元、3次元と次元を扱ってきましたが、ここでは次元を参照・変更するという関数について説明します。

次元数の参照：ndim

ndimはndarrayの次元数を参照することができます。

import numpy as np
 
a = np.array([1, 2, 3, 4])
print(a.ndim)
 
b = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
print(b.ndim)
 
c = np.array([[[ 1,  2,  3,  4], [ 5,  6,  7,  8], [ 9, 10, 11, 12]], 
              [[13, 14, 15, 16], [17, 18, 19, 20], [21, 22, 23, 24]]])
print(c.ndim)
 
# 表示結果 
# 1 
# 2 
# 3 

次元の入れ替え：transpose

transposeは引数で指定した順番通りに軸を入れ替える関数です
実際のコードで見た方が理解しやすいです

import numpy as np
 
a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
 
print(a)
print('----------')
 
b = a.transpose(1, 0)
print(b)
 
# 表示結果 
# [[ 1  2  3  4] 
#  [ 5  6  7  8] 
#  [ 9 10 11 12]] 
# ---------- 
# [[ 1  5  9] 
#  [ 2  6 10] 
#  [ 3  7 11] 
#  [ 4  8 12]] 

print('----------')は表示結果を見やすくするために入れています。
a.transpose(0, 1)と書いた場合は変化はありません。2次元の場合はa.transpose(1, 0)と書くことで軸が入れ替わります。

3次元である画像にtransposeを適用した例を見てみましょう

import cv2
 
image_file = 'cat.jpg'
img = cv2.imread(image_file)
 
cv2.imshow('image', img.transpose(1, 0, 2))
 
cv2.waitKey(0)
cv2.destroyAllWindows()

これは分かりやすい結果だと思います。

画像データは(高さ, 幅, カラーチャンネル)という並びであることを先ほど述べましたが、これを英語で書くと(Hight, Width, Channel)になります。この頭文字を取ってHWCと略します。
上記のコードではHWCからWHCへの変換したデータを表示しているということです。
HCW, WCH, CHW, CWHへの変換自体は可能です。ただし、それらの変換後データで画像表示を行うとエラーになりますので気を付けて下さい。

次回取り扱う推論エンジンの画像フォーマットはCHWです。そのためこのようなコードが必要になります

img = img.transpose((2, 0, 1)) # HWC > CHW 

次元の削減：squeeze

squeezeは大きさが1である次元を削除する関数です。これも実例をみて確かめてみましょう
まずは、大きさが1である次元の例を書いてみます。

import numpy as np
 
a = np.array([1, 2, 3, 4])
print(a)
print(a.ndim)
print(a.shape)
print('----------')
 
b = np.array([[1, 2, 3, 4]])
print(b)
print(b.ndim)
print(b.shape)
print('----------')
 
c = np.array([[[1, 2, 3, 4]]])
print(c)
print(c.ndim)
print(c.shape)
 
# 表示結果 
# [1 2 3 4] 
# 1 
# (4,) 
# ---------- 
# [[1 2 3 4]] 
# 2 
# (1, 4) 
# ---------- 
# [[[1 2 3 4]]] 
# 3 
# (1, 1, 4) 

変数aは1次元、bは2次元、cは3次元のndarrayです
aは今まで通りのndarrayですが、bやcは余分に[ ]が付いているのが分かるかと思います。
これが大きさが1である次元を含んでいる状態です。

squeezeは簡単に言うと、この余分な[]を取り除き、次元を減らす関数です。
以下のコードでは先の全てのndarrayに対して、squeezeを加えてみた例です。

import numpy as np
 
a = np.array([1, 2, 3, 4])
a = np.squeeze(a)
print(a)
print(a.ndim)
print(a.shape)
print('----------')
 
b = np.array([[1, 2, 3, 4]])
b = np.squeeze(b)
print(b)
print(b.ndim)
print(b.shape)
print('----------')
 
c = np.array([[[1, 2, 3, 4]]])
c = np.squeeze(c)
print(c)
print(c.ndim)
print(c.shape)
 
# 表示結果 
# [1 2 3 4] 
# 1 
# (4,) 
# ---------- 
# [1 2 3 4] 
# 1 
# (4,) 
# ---------- 
# [1 2 3 4] 
# 1 
# (4,) 

aは元々、大きさ１の次元はないため変化ありませんが、bとcは余分な[]が消えているのが分かるかと思います。

次元の追加：expand_dims

expand_dimsは逆に大きさ１の次元を追加することができます。
キーワード引数としてaxis=0を書くことにより次元の追加先を0番目の軸（一番外側の次元）に指定することができます。

import numpy as np
 
a = np.array([1, 2, 3, 4])
a = np.expand_dims(a, axis=0)
print(a)
print(a.ndim)
print(a.shape)
print('----------')
 
b = np.array([[1, 2, 3, 4]])
b = np.expand_dims(b, axis=0)
print(b)
print(b.ndim)
print(b.shape)
print('----------')
 
c = np.array([[[1, 2, 3, 4]]])
c = np.expand_dims(c, axis=0)
print(c)
print(c.ndim)
print(c.shape)
 
# 表示結果 
# [[1 2 3 4]] 
# 2 
# (1, 4) 
# ---------- 
# [[[1 2 3 4]]] 
# 3 
# (1, 1, 4) 
# ---------- 
# [[[[1 2 3 4]]]] 
# 4 
# (1, 1, 1, 4) 

大きさ１の次元が追加されているのが分かるかと思います。
このようにいくらでも次元を増やすことができます。一見意味無いように思えますが、次元数のフォーマットを合わせる際に使います。

これでプログラミンの基礎は整いました。次回からいよいよInference Engineを使ったディープラーニング推論です！
以上、「NumPy基礎プログラミング」でした。